Exponenciales

Existe otra función matemática muy importante, conocida como exponencial. La forma canónica de una función exponencial es la siguiente:

$$f(t)=Ae^{-t/\tau}, t \geq 0$$ (3.9)

$A$ corresponde a la amplitud máxima de la exponencial y $\tau$ se conoce como la constante de tiempo de la exponencial. La constante de tiempo es el tiempo que demora la exponencial en decaer $1/e$, es decir:

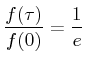$$\frac{f(\tau)}{f(0)}=\frac{1}{e}$$ (3.10)

La figura 1.5 muestra el gráfico de una función exponencial para $A=1$ y $\tau=1$. En la ecuación 1.9 e es el número de Euler, el cual tiene el valor irracional 2.718... y constituye la base de los logaritmos naturales. Este número es uno de los más importantes y fascinantes de la matemática y puede calcularse como:

$$e = \sum_{k=0}^\infty \frac{1}{k!} = \lim_{n\to 0} (1 + \frac{1}{n})^n \approx 2.718...$$ (3.11)

Figura 1.5: Función exponencial

El decaimiento exponencial ocurre naturalmente cuando una cantidad está decayendo a una tasa proporcional a lo que aún queda por caer. En la naturaleza, todos los resonadores lineales, tales como las cuerdas de los instrumentos musicales y los instrumentos de vientos exhiben un decaimiento exponencial en su respuesta a una excitación momentánea. La energía reverberante en una sala de conciertos decae exponencialmente una vez finalizada la emisión de sonido. Esencialmente todas las oscilaciones libres (sin una fuente mantenida en el tiempo) caen exponencialmente siempre que sean lineales e invariantes en el tiempo. Ejemplos de este tipo de oscilaciones incluyen la vibración de un diapasón, cuerdas pulsadas o pellizcadas y barras de marimba o xilófonos.

El crecimiento exponencial ocurre cuando una cantidad crece a una tasa proporcional al incremento actual. El crecimiento exponencial es inestable dado que nada puede crecer para siempre sin llegar a un cierto nivel límite.

Es necesario notar que en la ecuación 1.9, una constante de tiempo positiva implica a un decaimiento exponencial mientras que una constante de tiempo negativa corresponde a un crecimiento exponencial.

En sistemas de audio, una decaimiento de $1/e$ se considera muy pequeño para aplicaciones prácticas, como por ejemplo, para el diseño acústico de salas de concierto. Por lo general, se utiliza una cantidad tal que asegure que la señal ha caído 60 decibelios (dB). Esta cantidad, denotada por $t_{60}$, se encuentra resolviendo la ecuación:

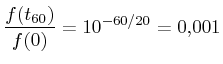$$\frac{f(t_{60})}{f(0)}=10^{-60/20}=0.001$$ (3.12)

Usando la definición de exponencial de la ecuación 1.9, se tiene entonces que:

$$t_{60}=\ln(1000)\tau \approx 6.91\tau$$ (3.13)

Esta ecuación nos dice que la constante $t_{60}$ es aproximadamente 7 veces la constante de tiempo $\tau$. Esto puede verificarse en la figura 1.5, donde se aprecia la ubicación de dicha cantidad en el eje del tiempo.