Sinusoides

La sinusoide es una de las señales más simples e importantes que existen. Las dos funciones matemáticas sinusoidales básicas son las funciones seno y coseno, las cuales están derivadas de las funciones trigonométricas del mismo nombre.

Matemáticamente una función de este tipo se puede escribir como:

$$f(x)=A\sin(wx+\phi)$$ (3.3)

o como

$$f(x)=A\cos(wx+\phi)$$ (3.4)

La amplitud $A$ corresponde a la desviación máxima de la señal respecto del origen (posición de equilibrio). La frecuencia $w$ corresponde a la cantidad de ciclos que existen en un determinado rango de la variable x. La fase, denotada por la letra $\phi$, corresponde a la desviación o corrimiento de la señal respecto del eje Y.

Una señal simple, de tipo sinusoidal, está completamente determinada por estos tres parámetros: amplitud, frecuencia y fase.

Ambas funciones, seno y coseno, son cíclicas o periódicas, es decir, vuelven a tomar los mismos valores después de un cierto rango de valores de la variable independiente.

Por ejemplo, la función seno es una función que vale 0 cuando la variable independiente vale 0, 1 cuando ésta vale $\pi/2$, 0 cuando pasa por $\pi$, -1 cuando cruza en $\ 3\pi/2$ y nuevamente cero cuando la variable independiente vale $2\pi$.

Figura 1.4: Funciones seno y coseno

[Función seno] [Función coseno]

La función coseno es muy similar a la función seno, sólo que está "desfasada" en relación al eje Y. En relación al desfase, Las siguientes relaciones matemáticas se cumplen entre estas funciones:

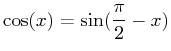$$\cos(x) = \sin(\frac{\pi}{2}-x)$$ (3.5)

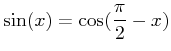$$\sin(x) = \cos(\frac{\pi}{2}-x)$$ (3.6)

La función seno es un función impar, es decir, no es simétrica respecto al eje Y. Matemáticamente esto es:

$$\sin(-x) = -\sin(x)$$ (3.7)

En cambio el coseno es una función par, porque es simétrica respecto al eje Y. Matemáticamente, esto equivale a:

$$\cos(-x) = \cos(x)$$ (3.8)

Las sinusoides son fundamentales para la física en general y la acústica en particular. Cualquier cosa que resuene u oscile produce un movimiento de tipo sinusoidal. Un ejemplo de esto es la oscilación de un péndulo, conocida como movimiento armónico simple.

Otra razón de la importancia de las sinusoides es que constituyen funciones básicas de los sistemas lineales. Esto significa que cualquier sistema lineal puede ser estudiado a través de su respuesta a funciones sinusoidales. En el campo del audio, las sinusoides son importantes para el análisis de filtros tales como reverberadores, equalizadores y otros tipos de efectos.

Desde un punto de vista matemático, las sinusoides constituyen bloques fundamentales que al ser combinados de cierta forma permiten la creación o síntesis de cualquier tipo de señal, por muy compleja que sea.

Pero quizás la razón más importante es que el sistema auditivo humano funciona como un analizador de espectro, tal como se detalla en el capítulo 3. Esto es, el oído humano físicamente separa un sonido en sus componentes de frecuencia sinusoidales. Por lo tanto, el oído humano funciona en forma muy similar a un analizador de Fourier (ver sección 1.2) y la representación de un sonido en el dominio de la frecuencia (ver sección 1.2.4) es mucho más cercana a lo que nuestro cerebro recibe que la representación temporal.